A/B test significance

​

What are we trying to figure out?

When we run an A/B test — like comparing static and interactive emails — we want to know: That’s where statistical significance comes in.

​

the setup

Let’s say we test two groups: Group A looks better — but the difference is tiny. Is it real, or could it just be random?

​

How to answer this question

We use a simple method called a Z-test to calculate a P-value. Here’s the step-by-step:

​

1. Pooled Conversion Rate

Combine both groups into one average baseline: $CVR_{pooled}= \frac{(Conversions_A + Conversions_B)}{(Group\ Size_A + Group\ Size_B)}$ For our example: $CVR_{pooled}= \frac{(10+8)}{(10057+10003)} =0.09\%$

​

2. Standard Error (SE)

This tells us how much natural randomness we expect between two similar-sized groups: $SE = \sqrt{CVR_{pooled} (1-CVR_{pooled})(\frac{1}{Group\ Size_A} + \frac{1}{Group\ Size_B})}$ For our example: $SE = \sqrt{0.09\% (1-0.09\%)(\frac{1}{10057} + \frac{1}{10003})}=0.04\%$

​

3. Z-Score

The Z-score shows how far the difference between two groups is from zero in terms of standard errors (zero being what we’d expect if there were no real difference). We calculate it by dividing the difference in conversion rates by the standard error — our expected random variation from sampling. $z = \frac{(CVR_B - CVR_A)}{SE}$ For our example: $z = \frac{(0.08\% - 0.10\%)}{0.042\%}=-0.46$ In simple terms, it answers:

“How unusual is this difference if A and B were actually performing the same?”

• If the Z-score is close to 0, the difference is small compared to the noise — probably just random chance.
• If the Z-score is 2 or more, the difference is much larger than the noise — likely not random, and therefore statistically significant.
• For this, we assume a standard normal distribution, i.e. 68% of all data falls between $z=-1SE$ and $z=+1SE$, and 95% between $z=-2 SE$ and $z=+2 SE$.

The Z-score converts into a p-value, telling us how likely such a difference could occur by chance.

​

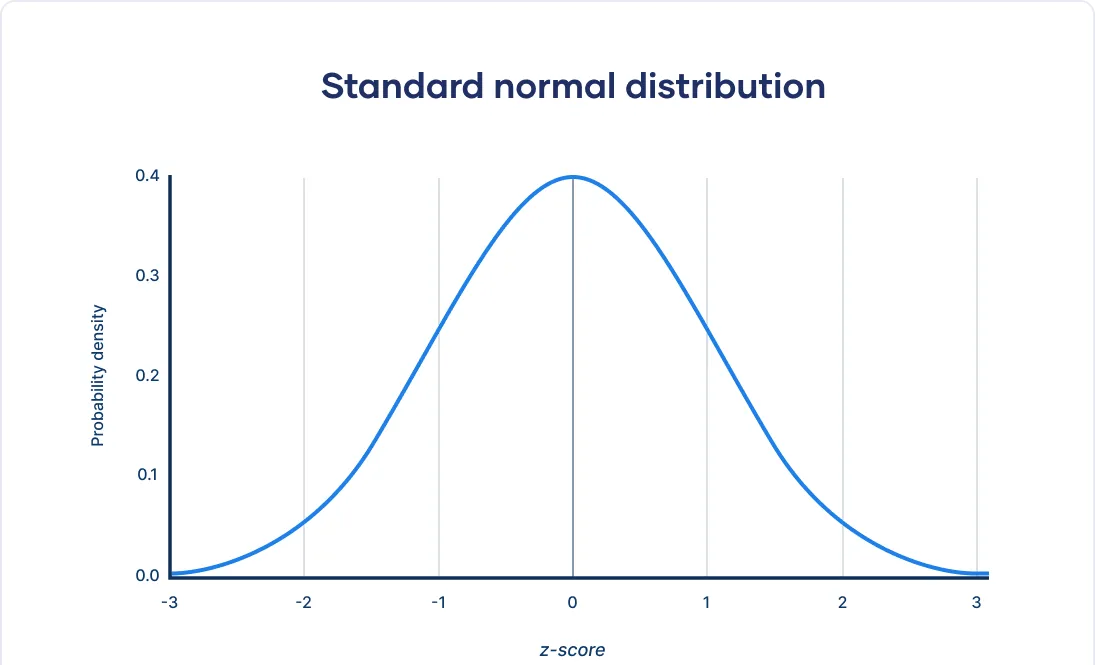
4. P-Value (Two-Tailed Test)

The p-value tells us how likely we’d see a difference this large (or larger) between A and B if they were actually identical — that is, if the difference was purely random. $p= 2 * (1-\Phi(|z|))$ Where $\Phi(|z|)$ is the cumulative distribution function of the standard normal distribution (the probability that a value is less than z). $p= 2 * (1-\Phi(|-0.47|))=0.65$ Put simply, it answers: Here’s how to interpret it:

• If the p-value is high (e.g. 0.65), there’s a 65% chance the difference is just random noise — making it not statistically significant.
• If the p-value is low (typically below 0.05), there’s less than a 5% chance it’s due to randomness — making it statistically significant.

We usually use 0.05 (5%) as the threshold for confidence.

​

What does this mean?

If your test result is significant, you can say: If it’s not significant, you say: For our example:

​

Important notes